格子上の場の理論

場の量子論とは？

量子力学と相対性理論を融合すると、場の量子論と言われる理論形式に到達する。場の量子論と言う名前は、量子力学で扱っていたものが電子や原子などの粒子であったのに対して、空間、時間の４次元空間の各点で定義される場を量子化した理論であることに由来している。身近な”場”の例の一つとしては電磁場 $\vec{E}(t,\vec{x}), \vec{B}(t,\vec{x})$ が挙げられる。場の量子論の場合、電磁場だけではなく、電子などの粒子に対応する波動関数 $\psi$ を場 $\psi(t,\vec{x})$ と考え、それをも量子化する。つまり、電子を量子化すると波動関数が現れ、その波動関数をもう一度量子化するのが場の量子化であり、このことから、場の量子化のことを”第２量子化”と呼ぶこともある。場の量子論の特徴は、物理的には、粒子の生成消滅を許す理論、ということであり、数学的には、非可算（数えられない）無限自由度の系の量子力学、ということである。場の理論は素粒子を支配する基本法則であると考えられている。

場の量子論の定式化としては、場の量の運動方程式を規定するラグランジアンから出発する経路積分の方法が一般的である。例えば光子と電子の相互作用を記述するQEDの場合ラグランジアンは、 $A_\mu(t,\vec{x})$ を光子場、 $F_{\mu\nu}=\partial _\mu A_\nu-\partial _\nu A_\mu$ を電磁場の強さ、 $\psi(t,\vec{x})$ を電子場として、

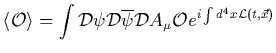
$\displaystyle {\cal L}(t,\vec{x}) =-\frac{1}{4}F_{\mu\nu}(t,\vec{x})F^{\mu\nu}(... ...gamma^\mu\left(\partial _\mu-igA_\mu(t,\vec{x})\right)-m\biggr] \psi(t,\vec{x})$ と書かれる。そして、ある場の量 ${\cal O}$ の期待値は経路積分により次のように書かれる。 $\displaystyle \left\langle \cal O \right\rangle = \int {\cal D}\psi {\cal D}{\overline{\psi}}{\cal D}A_\mu {\cal O} e^{i\int d^4x {\cal L}(t,\vec{x})}$ ここで $\int{\cal D}\psi$ とあるのは、時空間のあらゆる点における場 $\psi$ について積分すると言うことである。この経路積分を具体的に実行することが、場の量子論における究極の目標である。

摂動展開 ( QED )

上に書かれた経路積分は実は数学的にはちゃんと定義されておらず、従って直接実行することは不可能である。そのかわり、場の量子論では主に”摂動展開”と呼ばれる計算方法が使われている。この方法は、解を厳密に求めるのが困難な場合に、相互作用の強さを示す結合定数に関して低次から順次展開して求めていく方法である。ある場の量の期待値を摂動展開によって計算する方法は、Feynman則と呼ばれる規則によって完全に定められており、具体的な数値を計算出来るのである。しかし、このFeynman則に従って計算をそのまま進めて行くと、ある段階で期待値 $\left\langle \cal O \right\rangle$ が無限大に発散してしまう。この発散してしまった $\left\langle \cal O \right\rangle$ の中から、実験値と比較すべき有限な物理量を抜き出してやる方法が``くりこみ''と呼ばれる操作である。このくりこみの操作と合わせて、摂動展開は完成された計算方法と言うことができる。

この摂動展開の方法が最も成功したのは”量子電磁力学”(QED)においてである。 QEDは電磁場と電子などの電荷を持った粒子の理論であり、摂動展開の結果と実験値との一致が非常に良い。”量子電磁力学”の成功により場の量子論の正しさが確立されたのである。

摂動展開の困難 ( QCD )

ところが、摂動論の方法は陽子や中間子など強い相互作用をする粒子の振舞いを記述するのにはあまり役立たなかった。陽子や中間子はクォークと呼ばれる基本的な素粒子の束縛状態と考えられており、クォークの振舞いを記述する場の理論は”量子色力学”( QCD )と呼ばれている。 ``素粒子って何だっけ？'' で説明したようにクォークにはアップ(u)、ダウン(d)、ストレンジ(s)、チャーム(c)、ボトム(b)、トップ(t)の６種類があり、それぞれのクォークは更に3色の色を持っている。例えばバリオンは、異なる三つの色を持つクォークを閉じ込めて作られるのである。 QCDは量子電磁力学に非常に似ており、電子に相当するのがクォーク $\psi_i(t,\vec{x})$ 、電磁場に相当するものがグルーオン $A_\mu^a(t,\vec{x})$ と呼ばれるものである。そして、そのラグランジアンはQEDのものと非常に良く似た形をしている。

は、３×３の行列である。さらにゲージ場の強さは、 $F_{\mu\nu}^a=\partial _\mu A_\nu^a-\partial _\nu A_\mu^a +gf^{abc}A_\mu^bA_\nu^c$ という複雑な形で与えられているが、これはQCDが非可換ゲージ理論と呼ばれる理論に属していることによるものである。

このようにQCDは、QEDのものと非常に良く似たラグランジアンを持っているのであるが、この理論ではQEDの場合に成功した摂動展開はあまり役立たなかった。この失敗は、QCDの結合定数が大きく、摂動展開が良い近似にならないこと、またQCDでは摂動展開不可能な非摂動効果が本質的に重要であること、に原因がある。したがって、摂動論に代る新しい計算方法を見つけることが必要になる。

格子上の場の理論とは？

場の量子論は非可算無限自由度の系の量子力学であり、数学的に大変難しい理論である。この困難は４次元時空が連続なために起こったので、それを避けるために連続な４次元時空間を離散的な点の集まりに変えたものが格子（時空）である。点と点の間の距離を格子間隔と呼ぶ。これはいわば、理論で考え得る”最小の長さ”に相当する。この離散的な格子上で場の理論を定式化したのが格子上の場の理論である。これは可算無限自由度の量子力学であり、連続の場の理論より、はるかに扱いやすい。格子上の場の理論の特徴は、経路積分が数学的にきちんと定義されており、そのため摂動展開以外の計算方法が可能なところにある。例えば、結合定数の逆数による展開（強結合展開）などを使うと、 QCD において直面した困難の一部を乗り越えることが可能になる。

格子QCD

lattice 格子上の理論はQCDにおいて最も成功を収めている。この理論を格子QCDと呼ぶ。格子QCDの成功は、強結合展開などの解析的方法だけでなく、モンテ-カルロ法を用いた数値計算により経路積分が直接実行可能になったことに依るところが大きい。

通常格子QCDでは、ターゲットとしているハドロンなどが十分入るだけの箱を持ってきて、この箱の中で起きる反応のみに限って計算を行うことにする。このように格子時空の拡がりをも有限にすることによって、場の理論は有限自由度の量子力学になり、場の理論の難解な経路積分はただの積分に単純化され、計算機の上にのせての数値計算が可能になる。計算機の能力の飛躍的な向上とともにクォークの閉込めの理解、陽子等のハドロンの質量計算など、数々の興味深い結果が得られてきている。

何を研究するの？

格子QCDを研究することで、クォークの閉込め、カイラル対称性の自発的破れ、クォーク-グルーオンプラズマを作り出す有限温度相転移など、摂動展開では理解できない現象を定性的に理解することが可能になった。さらに数値計算によって、クォークの束縛状態であるハドロンの質量の計算やその崩壊定数の計算を定量的に行い、実験値と比較できる数値をだすことが現在の格子QCDの研究課題である。

何が難しい？

CP-PACS 格子QCDの数値計算では格子間隔は有限であるが、我々が欲しい結果は格子間隔がゼロの極限のものである。したがって、幾つかの格子間隔で計算を行い、その結果を基にして格子間隔がゼロ（連続極限）へ外挿して、欲しい結果を求めなくてはならない。外挿を正確に行うには、数値計算における統計誤差や系統誤差をできるかぎり小さくしなければならず、現在のスーパーコンピュータをもってしても膨大な計算時間がかかる。

また、技術的な問題としてフェルミオン積分の問題がある。クォーク場を表す $\psi(t,\vec{x})$ はフェルミオン場であるため、その積分はGrassmann積分となる。この積分は数学的には何の問題もないが、実際の計算には技術的な困難が伴い、スーパーコンピュータを用いてさえも膨大な時間がかかることが知られている。このフェルミオン場の積分は物理的には、クォーク-反クォークの真空中からの対生成の効果を取り入れることに相当するのであるが、計算時間を減すためにその効果を無視したクエンチ近似と呼ばれる近似も使われる。このように格子QCDの数値計算には膨大な計算量が要求されるため、汎用のスーパーコンピュータを使うだけではなく、格子QCD専用の計算機を作って計算を行う必要がでてきている。実際、我々筑波大学のグループも専用計算機 CP-PACS を製作し、計算物理学研究センターに配置し、それを使って数多くの計算を行っている。

筑波大グループの研究

専用計算機CP-PACSを用いて、ハドロン質量やクォークの質量、崩壊定数などの計算をクエンチ近似で行い、格子間隔ゼロへの外挿値を数％の誤差の範囲で求めた。このような高精度で連続極限への外挿を行ったのは世界ではじめてであり、その結果を実験値と比較することで、（１）ハドロン質量は１０％の範囲で実験値とクエンチ近似の結果とが一致すること（２）しかし、クエンチ近似の結果と実験値とのずれが数％の誤差の範囲を越えて存在すること、がわかった。つまり、クエンチ近似の妥当性の範囲とその限界を明らかにしたわけである。現在は、クォークの対生成の効果を正しく取入れた計算が進行中で、クエンチ近似と同様に、連続極限への外挿を行い、実験値と比較するつもりである。現在の計算はCP-PACSをもってしても1-2年はかかると思われる。この他にも、重いクォークの物理、有限温度や有限密度の物理、などの研究が行われている。

最近の研究結果については、年次報告を参考にしてほしい。また、日本物理学会の学会誌に投稿した記事 (postscript file)も参考になることと思う。

Back to Particle Theory Home Page