|
1a.単振動の微分方程式を解かせる よく知られているように微小振動は単振動で近似できます。 単振動の方程式を解けない人はいないと思いますが、今回は Mathematica でどうやって微分方程式を解くのかを、単振動を例にとって勉強します。 今回の提出課題 では速度に比例した減衰力がそこに加わった場合を考えてもらいます。 授業でやったことが理解できていれば難しくはありません。 |
| a)一般解を求めよう |
|
Mathematica で微分方程式を解くには DSolve[ ] を使います。 Mathematica に限らずアプリケーションは、いろいろ試しながら 覚えるのが上達の早道ですから、さっそく次のように入力してみましょう。
*以降このフォントは Mathematica の入力の意味に使います。
ここで、ギリシャ文字のオメガを入力するときは、Escキーを使いましょう。Escキーを一回押すと、三つの点々が出てくると思います。[Esc] omega [Esc]というように、Escキーで出た点々の内側にomegaと書くと、ギリシャ文字のオメガに変換されるはずです。 このように DSolve[ ] は引数を3つとります。 基本的な文法は DSolve[ eq, y[x], x ] です。 [Shift-Enter]を押すと次のようになるはずです。
*以降このフォントは Mathematica の出力の意味に使います。 DSolve[ ] は微分方程式の一般解を返してくれます。eq を {eq1,eq2, ... } にすれば連立微分方程式も解いてくれるし、x を {x1,x2, ... } にすれば偏微分方程式を解くこともできる賢い関数です。 |
| b) 特解を求めよう |
|
しかし一般解を求めただけでは物理の問題を解いたことにはなりません。 知りたい現象に見合った境界条件(または初期条件)に合致する特解まで 求めて、初めて解けたといえるわけです。さっそくやってみましょう。まず、
と入力してください。 ここでやってることの意味は、求まった一般解にx という名前をつけているだけです。 = は set の意味でしたね。== との違いがわかったでしょうか? あとで何度も利用するようなものには、こうやって名前をつけておくと便利です。 結果は、
となるだけです。(ちなみに、このように同じものを表示させるのを避けたい場合は、x=...の式の最後にセミコロン;を打ちましょう。) さて、Newton の運動方程式は2階微分方程式ですから、一般解に現れる 任意定数も2つです。したがってこれを消去するための初期条件も2つ必要で、 時刻 t=0 での x と x' を指定することにします。
|
| c) x' を求めよう |
|
そのための下準備として、まず x' を求めておきます。 x' = dx/dt は Dt[ x, t ] で表します。これもあとで利用することを考えて vという名前 をつけておきます。
ん? 結果をよく見ると、なんか変ですね。定数であるはずの c1, c2, ω でも微分してしまっています。仕方ないので t で偏微分することにしましょう。偏微分には D[ x, t] を用います。
今度はいいようです。所詮、機械が相手ですから、適当に対処してやる
必要がときどきあります。
v には改めて
次に t=0 での x と v (=x') を指定しましょう。 t の関数 f(t) へ t=0 を代入するような場合、ReplaceAll が使えます。ReplaceAll は /. と書きます。 具体的な文法は A /. B -> C で、「A の中に含まれる B をすべて C で置き換えろ」という意味です。実際やってみると、
となります。 |
| d)連立方程式を解こう |
|
次に x(0)=x0, v(0)=v0 という
2つの方程式を連立させて、c1, c2
を決定しましょう。
一般に Mathematica では何かを並べるとき、{a, b, c, ...} という形を使い、これをリストと呼びます。 %% は 2つ前の出力、% は前回もやったと おり直前の出力を意味します。あるいは
のようにすることもできます。%5 は 5番目の出力(Out[5])、%6 は 6番目の出力(Out[6])です。この5や6といった番号は、人によっては違うものになり得るので注意してください。 %などはちょっと計算する時は非常に便利です。しかし一方、Notebook を保存してあとで再利用しようと思ったときなど、整合性が取れなくなる 危険性もあることも事実です。実際、今やっている人のなかにも、 x(0)が %% や %5 に相当していない人もいるかもしれません。 確実なのは先程のように名前をつけておいてそれを利用する方法です。 今の場合なら、
ともあれ、これで積分定数も決まったので、特解が決まったことになります。 実際の関数形は、先ほどやった ReplaceAll を使って、
となります。ここでも ReplaceAll のルールを2つ同時に指定するため にリストを用いています。 |
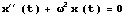 が解きたい微分方程式です。微分は '
で表せばよいことがわかると思います。また、
== は等しいという意味です。
= が 1個だと set (代入)の意味になるので、
意味がまるで違ってしまいます。
が解きたい微分方程式です。微分は '
で表せばよいことがわかると思います。また、
== は等しいという意味です。
= が 1個だと set (代入)の意味になるので、
意味がまるで違ってしまいます。