第五回レポート課題

まず、以下の数値データが与えられているとします。これはあるブラックホールのエネルギーを、格子模型を使ってモンテカルロ法による数値計算をして得られたデータです。 （このデータに関する詳しいことは、論文PRD94 no.8, 086010 (2016)に説明がありますが、以下ではプロットの方法だけに関してレポートを出題するため、格子模型の詳細や、計算方法などの詳細な内容を理解する必要はありません。しかし、一応大雑把に説明しておくと、このデータを得るにはまず時空を格子に分割して近似し、そこでブラックホールのエネルギーを計算したものだと思ってください。格子の間隔が狭くなる極限が、連続な時空におけるブラックホールに対応します。）

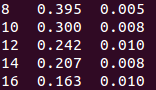
このデータの各列の数字の物理的意味は、以下の通りです。まず一列目(8,10,12...の列)は格子間隔の逆数1/aです。（つまり各行での格子間隔aはa=1/8, 1/10, 1/12...となっています。）２列目（0.395, 0.300...の列）は各格子間隔で計算されたブラックホールのエネルギー Eです。そして３列目（0.005, 0.008...の列）はそのエネルギー Eの誤差です。

このデータを、「横軸を格子間隔a、縦軸をエネルギーE」としてプロットすることを考えます。これに関して、以下のものを提出して下さい。ただし、上のデータファイルの名前はdata-report.txtとしてください。

(1) 次の[i],[ii]を実行するようなgnuplot上のスクリプト：[i] データを１次関数と２次関数によりfitする。[ii] fitで得られた関数と元のデータを一つの図にプロットする。
(2) 上の(1)のスクリプトを実行して得られる図
(3) fit.logにある、reduced chi-squareの定義やその意味についての解説
(4) (1)のfitに関して、誤差や(3)の解説に基づいた、fitの良し悪しについての考察
(5) 連続極限(a→0)におけるブラックホールのエネルギーEの推定値

注意点は以下の通りです。(1), (2)に関しては、出来上がる図が見やすくなるように工夫してください。このテキストで紹介したスクリプトを使ってできる図は、文字の大きさが不自然だったり、目盛も調節してなかったりと、お世辞にも良い図とは言えません。授業で紹介していないオプション等も各自で調べ、gnuplotの設定をフル活用して、できるだけ綺麗で独自性のある図にしてください。(3)については「これを読んだらreduced chi-squareが何なのか誰でも理解できる」というような、明快な解説を目指してください。(4), (5)も同様に、明快な解説を目指してください。