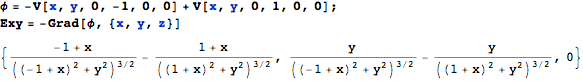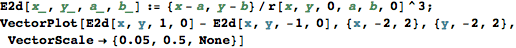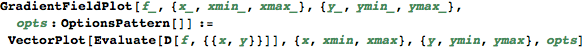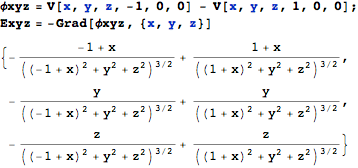|
1.電気双極子がつくる電場 今回はまず、前回取り上げた電気双極子を例に電場の視覚化を行います。 後半はより複雑な電気双極子が絡む静電場の問題で同様の視覚化を行います。 今回の提出課題 では、今回と前回の授業内容についての問題を各自でやってもらいます。
|
| a)ベクトル解析 |
|
Mathematica の古いバージョンでは、ベクトル解析を実行するためには VectorAnalysis` というパッケージを読み込む必要がありましたが、新しいバージョン では対応するパッケージがデフォルトで組み込まれています。 例えば、 内積 (Dot[ ])、外積 (Cross[ ] )、grad (Grad[ ] )、 div (Div[ ] )、rot (Curl[ ])、 Δ (Laplacian[ ] ) などの計算を行うことができます。詳しくはマニュアルを見てください。 さて、以下前回と同じユーザー定義関数を使います。
電気双極子として、座標(-1, 0, 0)に電荷-1、座標(1, 0, 0) に電荷+1を置いたものを仮定し、そのときの電場 (定義域をxy平面に限定したもの)を視覚化します。 電場と電位には E=-gradφ の関係があることを思い出すと、 電場を計算するには以下のようにすればよいことがわかります。
Grad のデフォルトの座標系は直交(カーテシアン)座標系です。例えば、極座標を使いたい時はオプションで指定します:
わかりにくい場合は具体的な関数で試してみましょう。 電場の話に戻ります。ベクトルはリストを使って表されることがわかります。 しかしアウトプットをよく見ると、2次元ベクトル場ではなく 3次元ベクトル場になっているので、これを2次元ベクトル場に変えて からプロットする必要があります。Take[ ] はリストからある部分を抽出してくれるので、これを使います。 (これはパッケージ VectorAnalysis` に含まれる 関数ではなく、デフォルトで使用できる関数です。)
似たような関数 Drop[ ] を用いて、Drop[Exy, -1] としても同じ結果が得られます。意味は「最後の要素を1個破棄しろ」です。 この種の関数で最も一般的なのは Part[ ] です。 これを用いて Part[Exy, {1,2}] としても同じ結果になります。Part はよく使われるため省略形が用意されており、 Exy[[{1,2}]] と書くこともできます。 |
| b) ベクトル場を視覚化する -- VectorPlot |
|
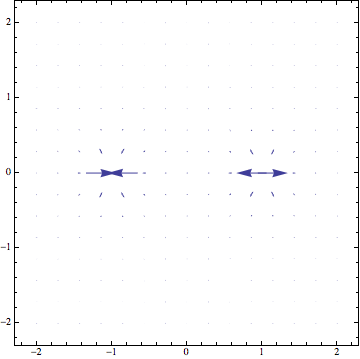
いずれを使用しても同じですので、ここでは例えば以下のように描画します。
あまり見やすくないので、オプションを使って見やすくしてみましょう。 例えば、
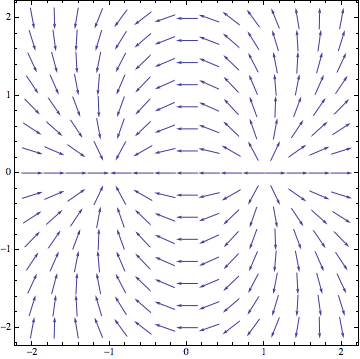
とすると
のようになります。オプションをいろいろ試してみて下さい。 あるいは、上のようにベクトル解析を使って電場を求めなくても、 電場の形はよく知られていますから、以下のように直接それを入力し てももちろん構いません。
Mathematica の古いバージョンでは、自動的に gradient を取ってベクトル場を表示するコマンド GradientFieldPlot/PlotGradientField がありました。同様のことを新しいバージョンで実行するには、コマンドを定義する必要があります:
このコマンドを用いると、電場を次のようにして描くことができます:
|
| c) ベクトル場を視覚化する (2) -- VectorPlot3D |
|
ベクトル場を3次元でプロットするには VectorPlot3D を用います。 まず、電場を計算します:
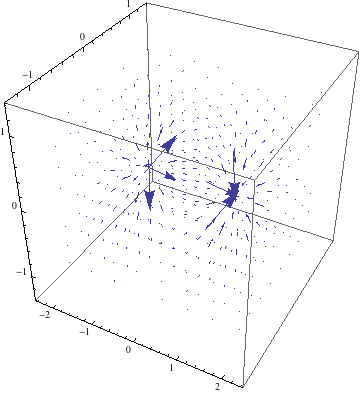
これをプロットするには次のようにします:
次のようにすると一気に実行できます:
Evaluate[] の中身を Grad[-φxyz, {x,y,z}] としても同様です。 他にもオプションを組み合わせて、各自で個性ある視覚化を行ってみてください。 |