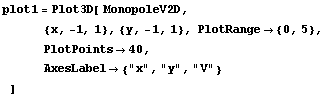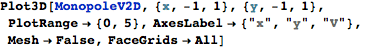|
1.点電荷の電位
今回は電位の視覚化を通して、Mathematica の3次元プロットを習得します。Mathematica の習得には、問題を解けるようになることとそれを視覚化できることの両方が重要ですが、簡単のために今回は問題を解く部分を省略し、グラフィックスに集中して勉強します。授業では点電荷に続いて、電気双極子が作る電位も取り上げます。
|
| a) ユーザー定義関数 |
|
物理の内容に入る前に、関数の定義の仕方を紹介します。Mathematicaにはもともと組み込まれた関数があります。例えば、Sin, Cos, Exp, Logなどです。また、近似値を求めるNや、因数分解するFactorも広い意味で関数といえるでしょう。一方で、自分で自由に関数を定義することもできます。例えば、f(x)=2x+3という関数を定義したいときは、 f[x_]:=2 x+3 [Shift-Enter]とします。ここで、等号の左にコロン(:)、そして左辺のxの右にアンダーバー( _ )がついているのに注意してください。:=は定義するという意味で、数学でもよくつかわれる記号です。一方でアンダーバーはMathematica特有の記法です。細かいことはさておき、とにかく関数の定義はこのようにするものだ、と覚えておきましょう。 (例1) xを3乗する関数cube[x]は以下のように定義できます。 cube[x_]:= x^3 [Shift-Enter]練習問題
|
| b) 電位の定義 |
|
さて、物理の話に移りましょう。座標 (a, b, c) に置かれた点電荷 ( 電荷は+q ) がつくる電位Vは
で表されます。ここで
となるCGS単位系を用い、この単位系のユニットで電荷が+1であると考えれば、
です。このような関数を Mathematica 上で定義するには、 次のようすればいいですね。
1行目で関数 r を、2行目では r を使って関数 V を定義しています。 1行目の最後にある;(セミコロン)は、入力をまとめて行う ときに使います。 (hogehoge1; hogehoge2; ... は前から順番に評価され、 最後のものについてのみ出力が行われます。) |
| c) 点電荷の電位 |
|
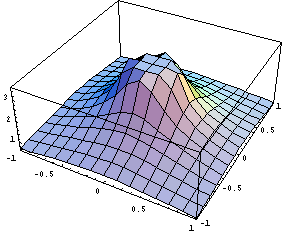
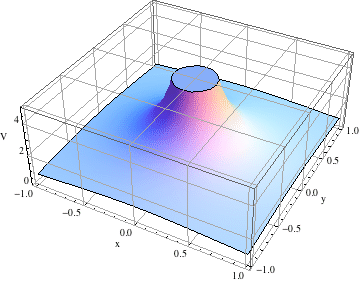
3次元プロットには Plot3D[ ]を用います。 V は3次元空間で定義された関数なので、そのままでは視覚化できません。 (z軸には V そのものをプロットしたいので。) そこで関数の定義域をxy平面に限定します。すなわち z=0 と置きます。ついでに点電荷は原点にある、すなわち (a,b,c)=(0,0,0) と仮定すれば、以下のようにしてxy平面上の電位がプロットできます。
(注) このHPの図は古いMathematicaのバージョンで作成されたものなので、図がカクカクしています。最新のバージョンでは、より滑らかな図が表示されますので、その違いは気にせずに進めて下さい。
と入力すれば、以下のようになります。
ここで、PlotPointsというのは、図を書くために計算する点の数です。これが多い方が滑らかな図になりますが、多くしすぎると図を書くのに長い時間がかかるようになります。変化が激しい関数の場合はカクカクした図になりがちなので、PlotPointsを多くとるようにするのが良いでしょう。
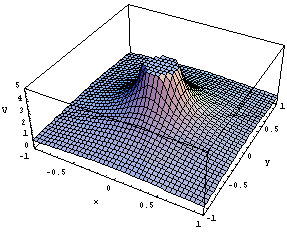
点電荷の電位は等方的なので、yz平面やzx平面を定義域に選んでも 同様の結果になります。また、原点で発散する関数形なので、原点を 含む面で図示する限り、すべてを図示することはできません。 |
| d)点電荷の作る等電位面 |
|
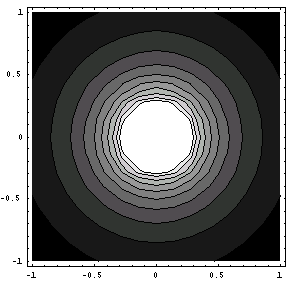
等電位面を描くには等高線プロットを行います。そのための関数は ContourPlot[ ] です。
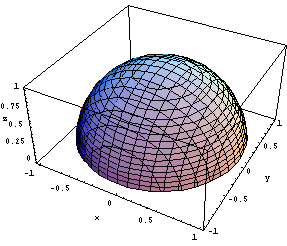
しかしこれでは等電位線であって、等電位面ではありません。 よくよく考えてみると、等高線のプロットをするときには、もはや定義域を2次元の平面に限る必要はありません。定義域を3次元にすれば、等電位面を描くことができます。そのための関数が ContourPlot3D[ ] です:
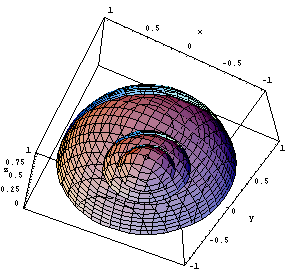
上の図で、Contour->{1,2,3}というオプションは、MonopoleV3Dの値が1,2,3となる等電位面を表示せよ、というものです。 ContourPlot3D は Graphics3D オブジェクトを生成します。 オプションの指定からわかるように、電位Vの値が1, 2, 3 である場所に 等高面を描かせていますが、これでは中が隠れてしまってよくわかりません。 z軸のマイナス方向から上を見上げれば様子がわかるはずなので、見る視点 (ViewPoint)を変えれば解決するはずです。
|