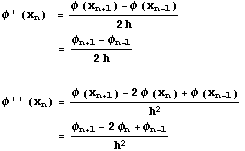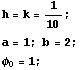|
第7回では常微分方程式を4次のRunge-Kutta法などを用いて数値的に解きました。 そのとき用いたアルゴリズムは大雑把に言って、ある初期値から出発し、 微小時間だけ時間発展した状態を逐次求めていくという方法でした。 しかし偏微分方程式の境界値問題を数値的に扱う場合、 一般にはこれらのアルゴリズムがうまく適用できない場合があります。 前回見たように Laplace 方程式は変数分離法を適用できる構造をして いたため常微分方程式の組に還元できましたが、 一般的にはそうとは限らないからです。 今回は前回に引き続き Laplace 方程式を題材に取り上げますが、 変数分離法を使わず直接偏微分方程式を数値的に解くことを考えます。 |
|
| a) 有限差分法(アルゴリズム) | |
|
境界値問題に対する数値解法はいろいろ考案されていますが、 ここでは有限差分法を取り上げます。 原理的には微分方程式を差分方程式に変換しその解を求めるという方法です。 この方法は複雑な境界条件を持つ問題には有効ではありませんが、 境界条件が比較的単純な場合に対しては高精度な計算が可能です。 まず、差分方程式にする部分を解説します。前にもやったように、閉区間 [a,b] を等間隔なN個のセグメント(幅を h とする)に分割します。 x0 = a, xN = b, xn = x0 + n h (n=1,2,....,N-1) [a,b] で定義されている関数 φ(x) の微分は、φの x-h および x+h のまわりでのTaylor展開の高次の項を無視すれば
となります。また2階微分は上の式を2回適用してやれば
となります。ただし導関数は任意の2点でのTaylor展開から定義できる ことを利用して 2h を改めて h と置いています。最初に定義した xnを利用すれば
と書けることになります。よってカーテシアン座標系でのLaplace方程式
はx方向のセグメントの幅を h、y方向のセグメントの幅を k とすれば、
と差分化できます。これは (N-1)2 個の未知数 (φ1,1, φ1,2,..., φN-1,N-1) に対する(N-1)2 個の独立な線型方程式であり、したがって原理的に解くこと が可能です。 実際にやってみたほうがわかりやすいと思うので、 前回と同じ問題を考えてみましょう。 |
|
| b) 有限差分法でLaplace方程式を解く(カーテシアン座標系) | |
セグメントの幅を
すなわちx方向に10分割、y方向に20分割することになります。 Laplace方程式は
です。境界条件は
と表せます。 リストを出力する関数 Table[ ] を利用して、(10-1)×(20-1)個の線型方程式は
によって生成することができます。 閉区間の両端では差分方程式が定義できない ため除かなければなりませんから、i は 0 からではなく h から始まって a-h まで、h ずつ増えていくように指定してあります。 j についても同様です。出力は冗長なので省略しますが、よく見ると 単一のリストになっていません。そこで同じく前出の リストをフラットにする関数 Flatten[ ] を利用して、
とすればよさそうです。ついでに個々の線型方程式に Simplify をかませて整理してあります。 連立方程式は Solve[ ] で解くことができますが、 その入力の手間を省くために変数も Table[ ] を使って生成してしまいましょう。
これらを使って
とやれば多少時間がかかると思いますが、解を得ることができます。 |
|
| c)視覚化 | |
|
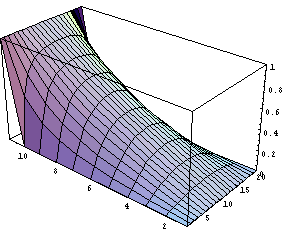
どんな解が求まったのか、いつものようにお絵描きしてみましょう。 スカラーポテンシャルφは、 0 <= i <= a, 0 <= j <= b で定義されていますから、範囲を変えてφ[i,j] を Table[] を使って生成し、そこに上で求まった解を適用してやります。
境界条件とあわせてこれですべての格子点上でφが決まったことになります。 リスト形式で定義された関数を3次元プロットするには ListPlot3D を使います。 使い方は Plot3D とほぼ同じですが、リストの格子点をそのまま 用いてプロットするため、PlotPoints をより細かいものに変更したりはできません。 関数 Interpolation[ ] を使って補間することも可能ですが、ある程度は Mathematica が自動的にやってくれますから何もしないでも充分だと思います。
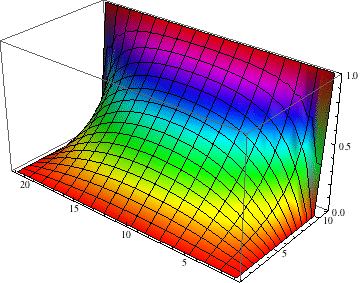
などとプロットできます。しかし、使用したオプションは先週のものに準じ ているはずなのに、結果が違うように見えます。実はリスト potential は (20+1)×(10+1)の行列なのですが、Mathematica は勝手に"行"、すなわち(20+1) のほうを x軸に選び、"列"、すなわち(10+1) のほうをy軸に選んでしまってい るために、プロットの段階でxとyが逆になってしまっています。 オプションの数字を変えるのは面倒なので、リストのほうを転置行列にし てしまいましょう。
Transpose[ ] が転置行列を求めるための関数 です。実際の行列の形をわかりやすい形で確認するには
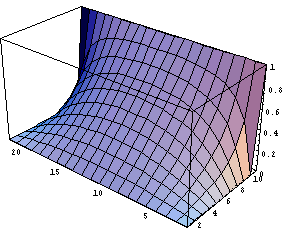
などとしてみてください。時間が限られているため今まで線型代数を 取り上げられませんでしたが、ベクトルや行列に関する計算も Mathematica には豊富にそろっています。例えば、 逆行列を求めるのは Inverse[ ]、 対角和や行列式を求めるにはそれぞれ Tr[ ] と Det[ ] です。 固有値問題を解くための関数も強力で、 Eigenvalues[ ]、 Eigenvectors[ ]、 Eigensystem[ ] があります。 グラムシュミットの直交化(関数 GramSchmidt) なども行えます。 話がそれましたが、転置行列をプロットしてやれば前回と同様の図
を描くことができます。もちろん偏微分方程式を差分方程式で近似 したわけですから、当然誤差が生じていることには注意が必要です。 しかし、前回のように無限和を有限和で置き換える必要がなかったため、 スムーズな絵になっていることがわかると思います。 蛇足ですが、 関数がリスト形式で与えられている場合の2次元プロットには ListPlot、等高線プロットには ListContourPlot、 濃淡グラフを描くには ListDensityPlot が用意されています。また濃淡グラフは 適当にオプションをつかって
のように 3次元プロットとともに描くことも可能です。
|
|
| d) Successive Over-Relaxation (SOR)法 | |
|
有限差分法を用いると、境界値問題が線型な連立方程式を解くという問題 に帰着することがわかりました。しかし、実際 Solve してみると、 たかだか 200×200 の行列の対角化でも、結構時間がかかることがわかります。 また、精度を改善しようとした場合、N×Nの行列の対角化の計算量は O(N3) に比例して急激に増大するため、大規模計算には向きません。 そこで、直接連立方程式を解くかわりに Successive Over-Relaxation (SOR) 法がよく用いられます。今回は実際にはやりませんが、流れだけ解説し ておきましょう。 今回のように h=k に選ぶなら、
は
となります。これを反復法により解くという方法です。
ω>1 の場合を Over-Relaxation (OR) 法といい、これを繰り返すことで収束した解を求めようという方法です。
最後に、まだまだやりたいことはたくさんあったのですが、1学期という短い間では Mathematica の概要を説明するのが精一杯でした。 この授業が今後の皆さんの物理や数学の学習のお役に立てれば幸いです。 |